El cuadrado mágico del papa León III
!no hay nada misterioso ni mágico en este cuadrado, sólo una serie de propiedades muy interesantes… pero ¡muy, muy interesantes!
El papa León III (750-816) redactó hacia el año 795 un opúsculo titulado Enchiridion, una recopilación de oraciones, regalo del papa al emperador Carlomagno.
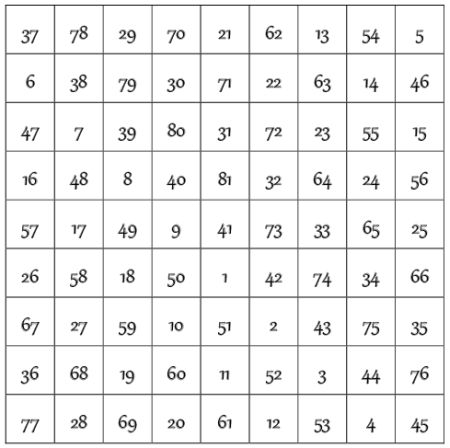
En este texto aparece un curioso cuadrado numérico, sin ningún comentario: es un cuadrado mágico de orden 9 y de constante mágica –suma de cada una de las 9 filas, de las 9 columnas o de las 2 diagonales– 369.
En muchas ediciones modernas del texto (por ejemplo, en la edición de 1660), este cuadrado se ha eliminado.
En Le Carré magique du Pape Léon III (Bibnum, septiembre de 2014), René Descombes –experto en cuadrados mágicos– realiza un exhaustivo análisis de las propiedades de este cuadrado papal. El artículo es extenso y precioso, sólo destaco debajo algunas de las propiedades:
1) La suma de los términos simétricos respecto al centro del cuadrado es constante e igual a 92 + 1 = 82 –la constante de polarización– y la casilla central es justo la mitad de esta constante 41.
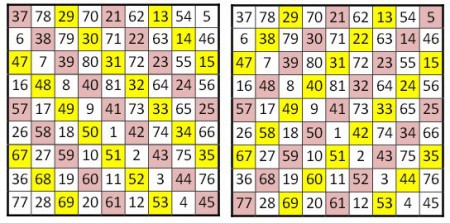
2) Si se observan las diagonales paralelas a la primera diagonal –la que va de la esquina izquierda arriba la esquina derecha abajo–, en una de cada dos sus términos son los de una progresión aritmética de razón 1. Sucede lo mismo para la otra diagonal; estas líneas están coloreadas en el dibujo de debajo:
3) Las columnas poseen una cierta regularidad en la diferencia entre términos adyacentes
4) Se obtiene el número mágico 369 con muchas otras combinaciones de 9 números aparte de las filas, columnas y diagonales
5) Es un cuadrado autocomplementario: cuando se reemplaza cada término de un cuadrado mágico de orden n por su complementario a n2 + 1 (es decir, se reemplaza aij por n2 + 1 – aij), se obtiene otro cuadrado mágico que se llama complementario del primero. En este caso (n=9) además, tras rotarlo 180 grados, este último se superpone con el cuadrado original
6) El cuadrado papal está formado por 9 subcuadrados de orden 3, que poseen también sorprendentes propiedades
En el artículo se explica también un método simple para construir el cuadrado papal y algunas otras propiedades interesantes.
No hay comentarios:
Publicar un comentario